Differentiable spike:Rethinking gradient-descent for training spiking neural networks

Abstract

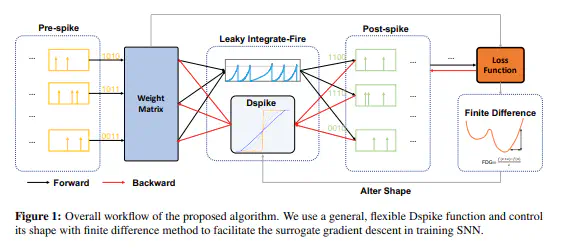
Spiking Neural Networks (SNNs) have emerged as a biology-inspired method mimicking the spiking nature of brain neurons. This bio-mimicry derives SNNs’ energy efficiency of inference on neuromorphic hardware. However, it also causes an intrinsic disadvantage in training high-performing SNNs from scratch since the discrete spike prohibits the gradient calculation. To overcome this issue, the surrogate gradient (SG) approach has been proposed as a continuous relaxation. Yet the heuristic choice of SG leaves it vacant how the SG benefits the SNN training. In this work, we first theoretically study the gradient descent problem in SNN training and introduce finite difference gradient to quantitatively analyze the training behavior of SNN. Based on the introduced finite difference gradient, we propose a new family of Differentiable Spike (Dspike) functions that can adaptively evolve during training to find the optimal shape and smoothness for gradient estimation. Extensive experiments over several popular network structures show that training SNN with Dspike consistently outperforms the state-of-the-art training methods. For example, on the CIFAR10-DVS classification task, we can train a spiking ResNet-18 and achieve 75.4% top-1 accuracy with 10 time steps.