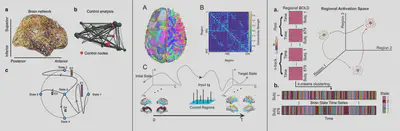
Brain Control Analysis

Cognitive function is driven by dynamic interactions between large-scale neural circuits or networks, enabling behaviour. However, fundamental principles constraining these dynamic network processes have remained elusive. Here we use tools from control and network theories to offer a mechanistic explanation for how the brain moves between cognitive states and how we can intervene the transition with predictable design.

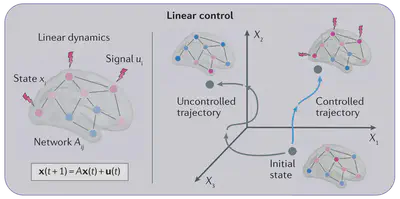
In network control, the system in question typically comprises a complex web of interacting components, and the goal is to drive this networked system towards a desired state by influencing a select number of input nodes. The starting point for most control-theoretic problems is the lineartime-invariant control system $$\mathbf{x}(t + 1) = \mathbf{A}\mathbf{x}(t) + \mathbf{u}(t),$$ where $\mathbf{x}(t)$ defines the state of the system (for example, the blood-oxygen-level-dependent signal measured by functional magnetic resonance imaging), $\mathbf{A}$ is the interaction matrix (for example, representing white matter tracts estimated using diffusion tensor imaging) and $\mathbf{u}(t)$ defines the input signal (such as electromagnetic stimulation using transcranial magnetic simulation or deep brain simulation). A system is called controllable if it can be driven to any desired state. often, however, many naturally occurring networks that are theoretically controllable cannot be steered to certain states owing to limitations on control resources motivating the introduction of control strategies $\mathbf{u}^*(t)$ that minimize the norm so-called control energy $E(\mathbf{u}) = \sum_{t=0}^{\infty}|\mathbf{u}(t)|^2$, where the notation $|·|$ denotes the $l^2$-norm.